Transiciones de fase en problemas computacionales aleatorios
Presentado por Ricardo Restrepo López
Instituto de Matemáticas, Universidad de Antioquia
Transiciones de fase en problemas computacionales aleatorios
Transiciones de fase en problemas computacionales aleatorios
En esta charla exhibiremos:
- Algunos resultados y técnicas.
- Solubilidad y complejidad algorítmica.
- Como modelo prototípico usaremos 2-coloramiento de hipergrafos.
2-coloramiento de hipergrafos
Un hipergrafo es una generalización del concepto de grafo, en el que una arista puede conectar cualquier número de vértices:
- Sistema de conjuntos (Teoría de Sperner)
- Estructura de incidencia (Geometría combinatorial)
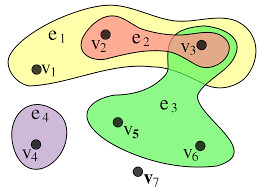
2-coloramiento de hipergrafos
Un hipergrafo es $k$ uniforme si cada arista es una $k$-tupla de vértices (no necesariamente diferentes).
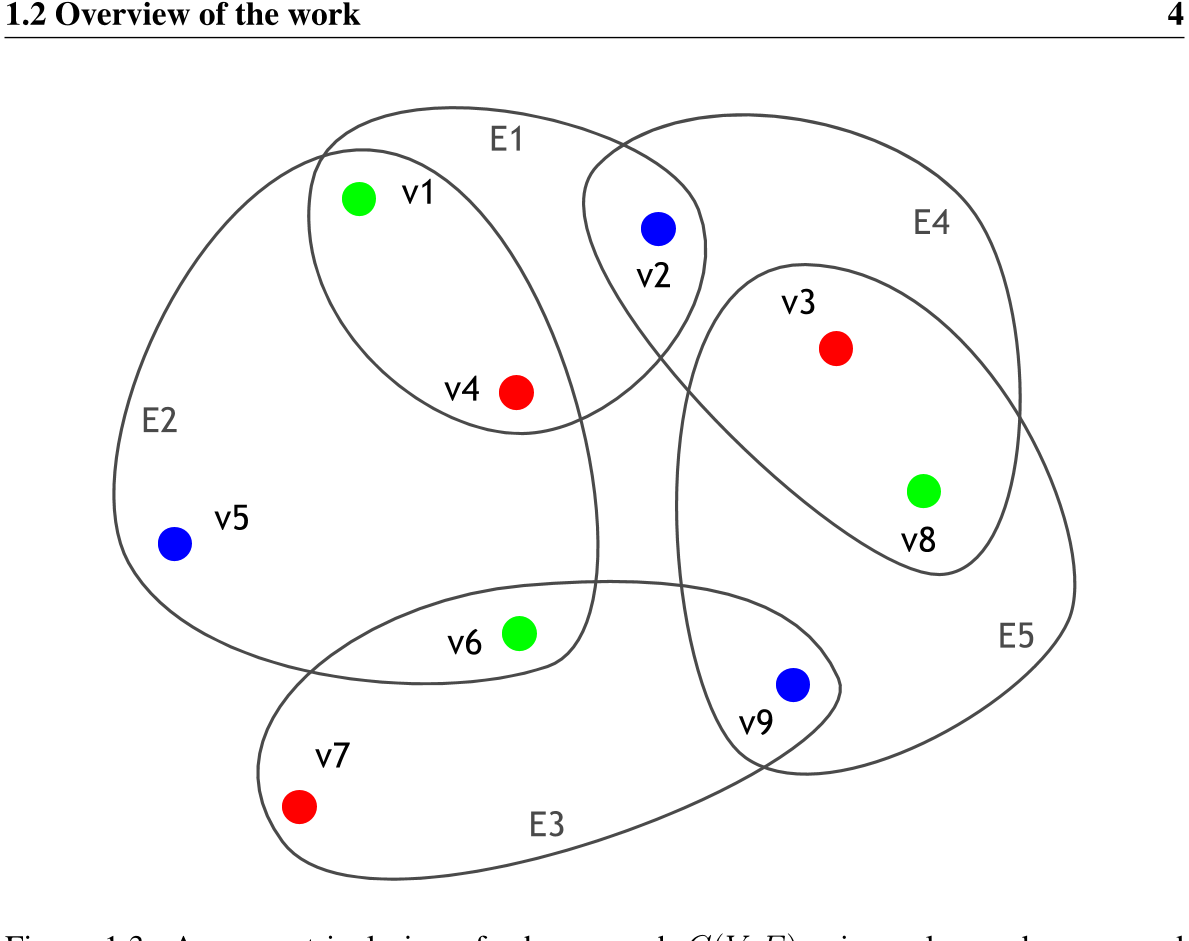
2-coloramiento de hipergrafos
La propiedad de ser 2-coloreable (propiedad B) ha sido estudiada desde el trabajo de Bernstein en 1908 en hipergrafos infinitos.
El problema de decisión es NP-completo
(Laslo Lovasz, 1973).
2-coloramiento de hipergrafos aleatorios
Un hipergrafo aleatorio $H_k(n,m)$ es un hipergrafo $k$-uniforme con $n$ vértices y $m(n)$ aristas aleatorias escogidas de manera independente e uniforme entre todas las posibles $k$-tuplas de vértices.2-coloramiento de hipergrafos aleatorios
Una propiedad de hipergrafos $P$ se dice que se satisface con alta probabilidad en el nivel $m(n)$ de aristas si \[ \mbox{lim}_{n \to \infty} \mathbf{P}[H_k(n,m) \mbox{ satisface } P ] = 1 \]2-coloramiento de hipergrafos aleatorios
Alon Spencer "The strange logic of random graphs".- Propiedades de primer orden son cerradas bajo inferencia lógica.
- Completez en ciertos casos de $m(n)$ (Ley $0$/$1$).
- Conectividad o colorabilidad no son expresables en primer orden. ¿Otros lenguajes?
2-coloramiento de hipergrafos aleatorios
Umbral de satisfabilidad.- Umbral fino: Conectividad.
- Umbral grueso: Existencia de un subgrafo 'pequeño'.
2-coloramiento de hipergrafos aleatorios
Ehud Friedgut y Jean Bourgain: Sharp thresholds of graph properties (1999)- Si una propiedad monótona tiene un umbral grueso, entonces puede ser aproximada por la propiedad de tener un subgrafo pequeño adecuado.
2-coloramiento de hipergrafos aleatorios
La propiedad B no puede ser aproximada por la propiedad de tener un grafo pequeño adecuado(Entonces tiene un umbral fino!).
- Localizar tal umbral. (Esto haría el problema de decisión, 'trivial')
- Estudiar umbral para propiedades del tipo: "El algoritmo $\mathbf{A}$ halla un 2-coloramiento del grafo en tiempo $O(n^d)$".
El lema local de Lovasz
Lovasz, Erdos (1973, 1975, 1977):- Sean $A_1, \ldots, A_t$ eventos con probabilidad acotada por $p$.
- Cada uno de ellos es independiente del álgebra de eventos generada por todos los demás excepto a lo más $d$ de ellos.
- Entonces, si $ep(d + 1) < 1 $, con probabilidad positiva, ninguno de los eventos ocurre.
2-coloramiento de hipergrafos aleatorios
- Alon y Spencer: Existe $c_k$ tal que si $m(n) = c 2^k n /k^2$ con $c < c_k$ entonces $H_k(n,m)$ es $2$-coloreable.
Método del primer momento
- Desigualdad de Markov: Si $X\geq 0$ entonces $P(X\geq 1) \leq \mathbf{E}[X]$
- Alon y Spencer: Si $m(n) = rn $ con $r> 2^{k-1} \ln{2} - \ln{2}/2$, entonces $H_k(n,m)$ no es $2$-coloreable.
Método del segundo momento
- Desigualdad de Paley-Zygmund: Si $X\geq 0$ entonces $$P(X > 0) \geq (\mathbf{E}[X])^2 / \mathbf{E}[X^2].$$
- Achlioptas, Moore (2002): Si $m(n) = rn $ con $r < 2^{k-1} \log{2} - \log{2}/2 - (1 + o_k(1)) / 2$, entonces $H_k(n,m)$ es $2$-coloreable.
Algoritmos
Algoritmo CR. (Chvátal, Reed):-
- Si hay aristas monocromáticas coloreadas parcialmente con $k-1$ o $k-2$ vértices:
- Sea $v$ el vértice no coloreado más pequeño de la arista más pequeña con la propiedad anterior.
- Coloree $v$ de tal manera que la arista $e$ sea bicromática.
- Si no hay tales aristas:
- Coloree los vértices no coloreados más pequeños, $v$ y $w$ de rojo y azul respectivamente.
Algoritmos
Algoritmo CR. (Chvátal, Reed):- (Achlioptas, Kim, Krivelevich, Tetali) (2000): Existe $c_k$ tal que si $m(n) > c 2^k n /k$ con $c>c_k$ la propiedad 'el algoritmo CR halla en tiempo lineal un 2-coloramiento' se satisface con alta probabilidad.
Algoritmos
- Versión algorítmica del lema Local de Lovasz: Beck (91), Alon (91), Molloy, Reed (98), Czumaj, Scheideler (00), Srinivasan (08), Moser, Tardos (08, 09).
- Existe $c_k$ tal que si $m(n) = c 2^k n /k^2$ con $c < c_k$ entonces $H_k(n,m)$ es $2$-coloreable en tiempo lineal.
Algoritmos
- Eliminación (Peeling, core): Pittel, Spencer, Wormald (96). Janson (2011).
- Para problemas de satisfacción: Montanari, Restrepo, Tetali (2011), Molloy, Restrepo (2012).
- Si $m(n) \geq \Omega(\alpha_k 2^k / k)$ entonces el core es vacío y el proceso de eliminación siempre halla un coloramiento.
Algoritmos
Estudio del core:- Aproximación por ecuaciones diferenciales (Wormald)
- Acoplamiento con procesos de Poisson (Janson)
- Desigualdad de Azuma.
Vertical Slides
Slides can be nested inside of each other.
Use the Space key to navigate through all slides.

Basement Level 1
Nested slides are useful for adding additional detail underneath a high level horizontal slide.
Basement Level 2
That's it, time to go back up.

Slides
Not a coder? Not a problem. There's a fully-featured visual editor for authoring these, try it out at http://slides.com.
Point of View
Press ESC to enter the slide overview.
Hold down alt and click on any element to zoom in on it using zoom.js. Alt + click anywhere to zoom back out.
Touch Optimized
Presentations look great on touch devices, like mobile phones and tablets. Simply swipe through your slides.
Fragments
Hit the next arrow...
... to step through ...
... a fragmented slide.
Fragment Styles
There's different types of fragments, like:
grow
shrink
fade-out
fade-up (also down, left and right!)
current-visible
Highlight red blue green
Transition Styles
You can select from different transitions, like:
None -
Fade -
Slide -
Convex -
Concave -
Zoom
Themes
reveal.js comes with a few themes built in:
Black (default) -
White -
League -
Sky -
Beige -
Simple
Serif -
Blood -
Night -
Moon -
Solarized
Slide Backgrounds
Set data-background="#dddddd" on a slide to change the background color. All CSS color formats are supported.

Image Backgrounds
<section data-background="image.png">Tiled Backgrounds
<section data-background="image.png" data-background-repeat="repeat" data-background-size="100px">Video Backgrounds
<section data-background-video="video.mp4,video.webm">... and GIFs!
Background Transitions
Different background transitions are available via the backgroundTransition option. This one's called "zoom".
Reveal.configure({ backgroundTransition: 'zoom' })Background Transitions
You can override background transitions per-slide.
<section data-background-transition="zoom">Pretty Code
function linkify( selector ) {
if( supports3DTransforms ) {
var nodes = document.querySelectorAll( selector );
for( var i = 0, len = nodes.length; i < len; i++ ) {
var node = nodes[i];
if( !node.className ) {
node.className += ' roll';
}
}
}
}
Code syntax highlighting courtesy of highlight.js.
Marvelous List
- No order here
- Or here
- Or here
- Or here
Fantastic Ordered List
- One is smaller than...
- Two is smaller than...
- Three!
Tabular Tables
| Item | Value | Quantity |
|---|---|---|
| Apples | $1 | 7 |
| Lemonade | $2 | 18 |
| Bread | $3 | 2 |
Clever Quotes
These guys come in two forms, inline:
“The nice thing about standards is that there are so many to choose from”
and block:
“For years there has been a theory that millions of monkeys typing at random on millions of typewriters would reproduce the entire works of Shakespeare. The Internet has proven this theory to be untrue.”
Intergalactic Interconnections
You can link between slides internally, like this.
Speaker View
There's a speaker view. It includes a timer, preview of the upcoming slide as well as your speaker notes.
Press the S key to try it out.
Export to PDF
Presentations can be exported to PDF, here's an example:
Global State
Set data-state="something" on a slide and "something"
will be added as a class to the document element when the slide is open. This lets you
apply broader style changes, like switching the page background.
State Events
Additionally custom events can be triggered on a per slide basis by binding to the data-state name.
Reveal.addEventListener( 'customevent', function() {
console.log( '"customevent" has fired' );
} );
Take a Moment
Press B or . on your keyboard to pause the presentation. This is helpful when you're on stage and want to take distracting slides off the screen.
Much more
- Right-to-left support
- Extensive JavaScript API
- Auto-progression
- Parallax backgrounds
- Custom keyboard bindings